Математическая оптимизация принятия решений
Мотивация
Внедрение методов математической оптимизации позволит компании значительно сократить издержки и повысить эффективность бизнес-процессов. Оптимизационные модели помогут находить наилучшие решения в сложных многокритериальных задачах, таких как управление запасами, маршрутизация логистики или распределение ресурсов, что приведёт к существенной экономии времени и денег. Кроме того, использование математических алгоритмов обеспечит гибкость и адаптивность бизнеса, позволяя быстрее реагировать на изменения рыночных условий и принимать обоснованные решения на основе данных, а не интуиции. Это не только даст конкурентное преимущество, но и повысит прозрачность процессов, позволяя выявлять и устранять узкие места в работе компании.
Кому будет интересно:
Подразделения компании, которым может быть интересна математическая оптимизация с указанием возможных сценариев
Маркетинг и реклама:
- Оптимизация контента для A/B тестов: Байесовская оптимизация для выбора лучшего рекламного креатива
- Моделирование LTV (Lifetime Value): Марковские цепи для прогнозирования ценности клиента
- Оптимальное ценообразование: Логистическая регрессия и нелинейная оптимизация для определения цен с учетом спроса
- Распределение маркетингового бюджета: Оптимизация на основе многоруких бандитов для эффективного тестирования каналов
Продажи:
- Оптимальное распределение скидок: Нелинейное программирование для максимизации прибыли с учетом эластичности спроса
- Оптимизация ассортимента: Линейное программирование для выбора наиболее прибыльных товаров
- Маршрутизация торговых представителей: Задача коммивояжера для минимизации времени на посещение клиентов
- Оптимизация рекламного бюджета: Линейное программирование для распределения затрат между каналами рекламы
Управление персоналом:
- Оптимизация графика работы сотрудников: Целочисленное программирование для минимизации переработок
- Оптимизация найма персонала: Линейное программирование для выбора кандидатов с учетом бюджета и компетенций
- Оптимизация обучения сотрудников: Байесовские модели для подбора индивидуальных программ обучения
- Прогнозирование увольнений: Модели выживаемости (Survival Analysis) для предсказания текучести кадров
Финансы и бухгалтерия:
- Оптимизация инвестиционного портфеля: Модель Марковица для нахождения оптимального соотношения риска и доходности
- Управление денежными потоками: Линейное программирование для минимизации кассовых разрывов
- Оптимизация кредитного скоринга: Логистическая регрессия и деревья решений для снижения риска дефолта
- Оптимизация налоговой нагрузки: Линейная оптимизация для распределения доходов и расходов по разным юрисдикциям
Производство:
- Оптимизация производственного графика: Алгоритм Джонсона для минимизации времени обработки заказов
- Оптимизация энергопотребления: Нелинейное программирование для сокращения затрат на электроэнергию
- Оптимизация запасов сырья: Динамическое программирование для минимизации дефицита и излишков
- Балансировка производственных линий: Целочисленное программирование для равномерного распределения загрузки станков
Логистика:
- Оптимизация маршрутов доставки: Алгоритмы Дейкстры и A* для сокращения расстояний
- Оптимальное управление запасами: Модель EOQ (экономичный размер заказа) для минимизации затрат на хранение
- Распределение товаров на складе: Линейное программирование для минимизации времени отбора
- Загрузка транспортных средств: Целочисленное программирование для оптимальной компоновки груза
IT:
- Оптимизация распределения серверных мощностей: Нелинейное программирование для минимизации затрат на облачные сервисы
- Оптимизация трафика в сети: Алгоритмы минимального остовного дерева для балансировки нагрузки
- Оптимизация тестирования ПО: Целочисленное программирование для выбора минимального набора тестов с максимальным покрытием
- Оптимизация базы данных: Генетические алгоритмы для настройки индексов и распределения запросов
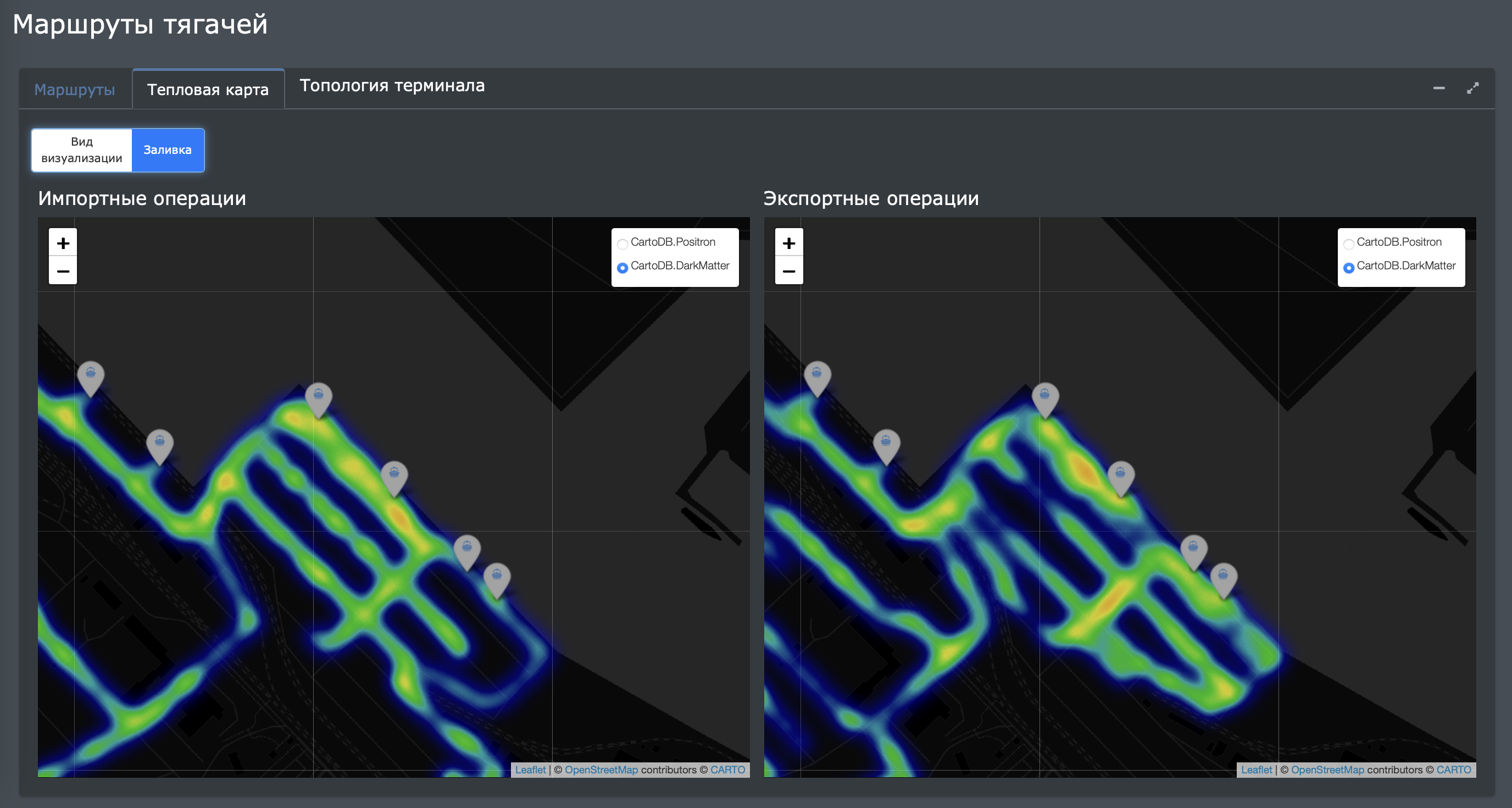
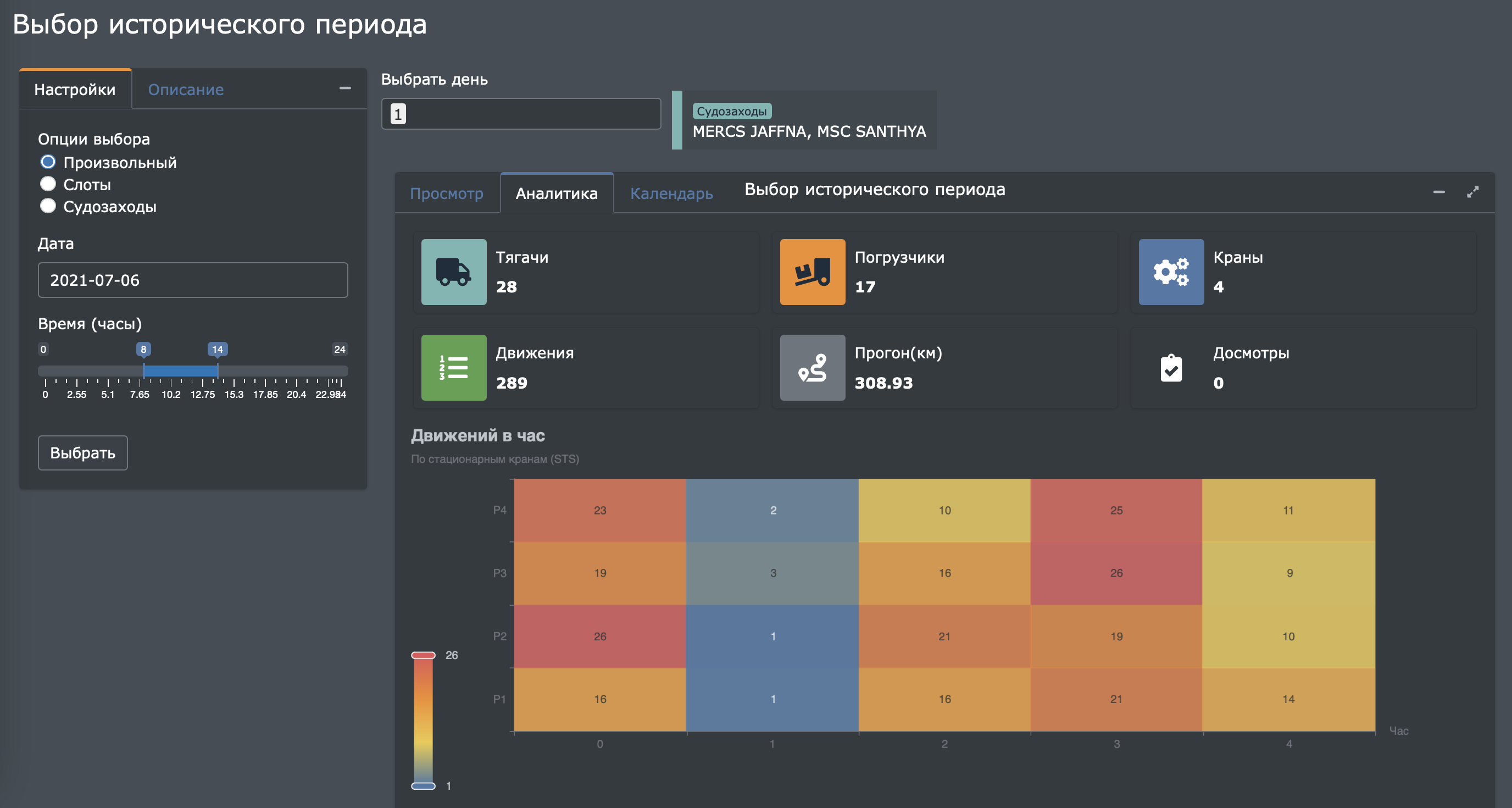
Кейс. Оптимизации работы контейнерного терминала
Задача
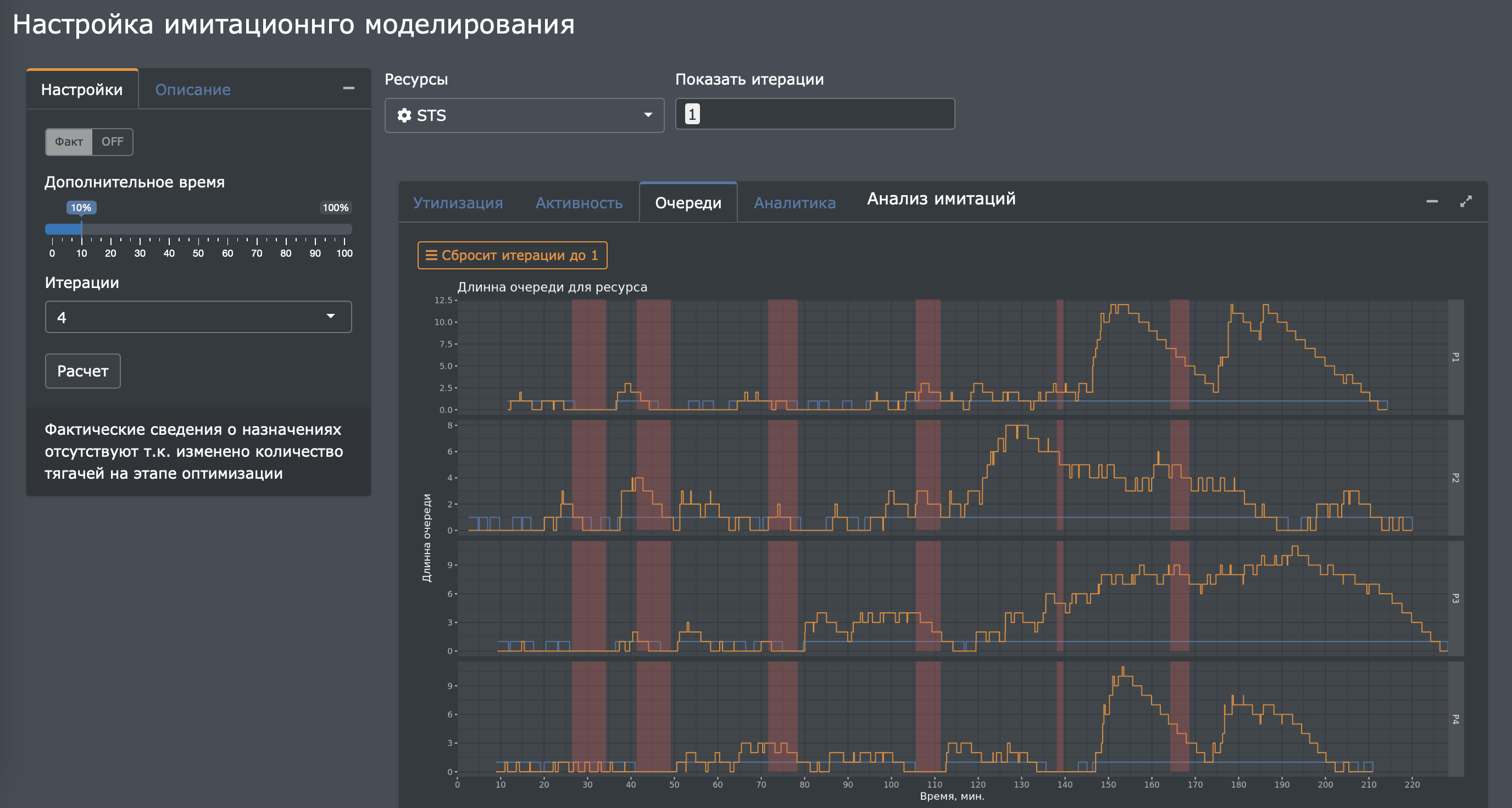
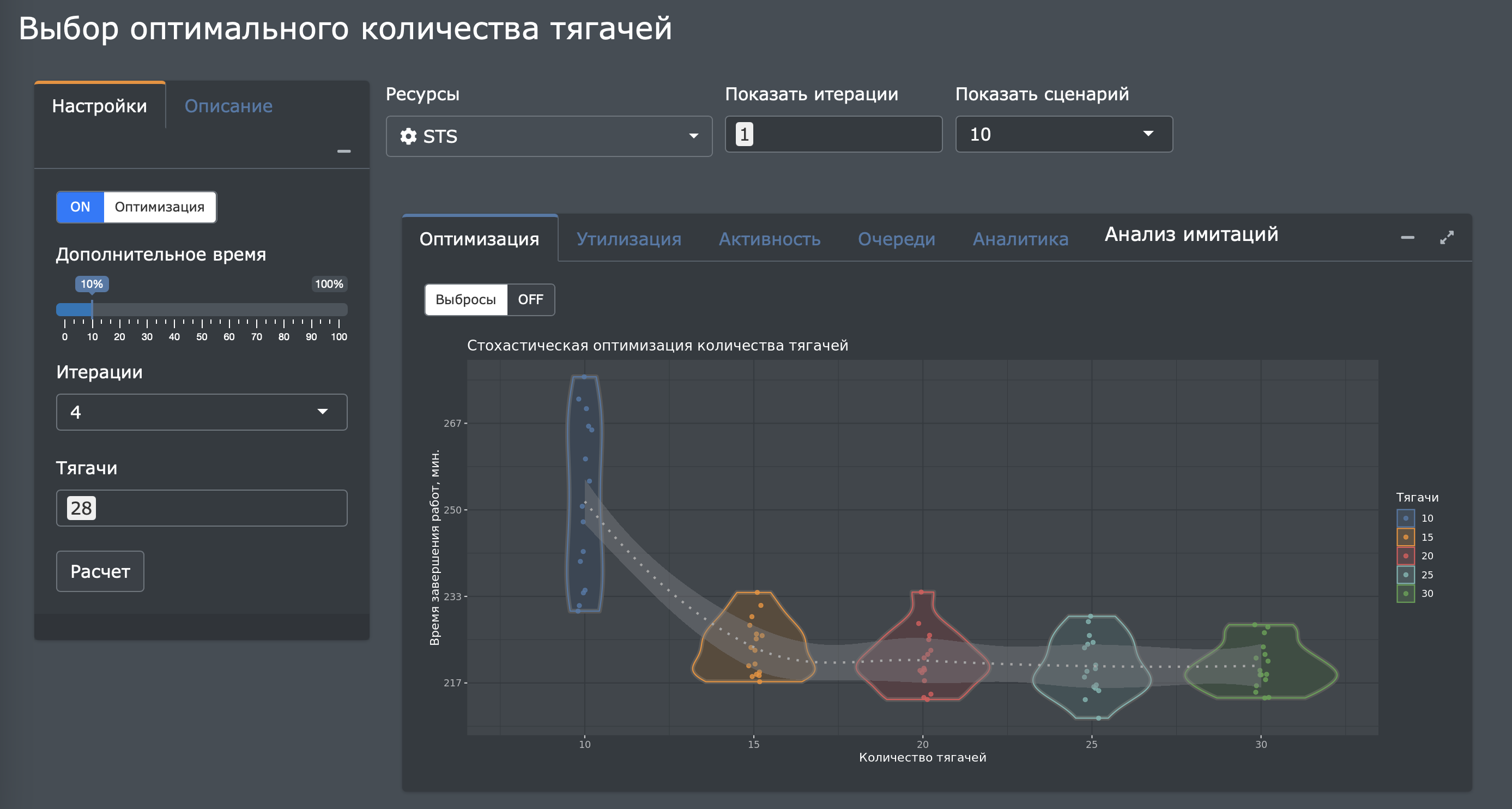
Крупный контейнерный терминал заинтересован в сокращении издержек, связанных с неоптимальным использованием производственных фондов (тягачей). Основными проблемами являлись простои тягачей и порожняковый пробег.
Решение
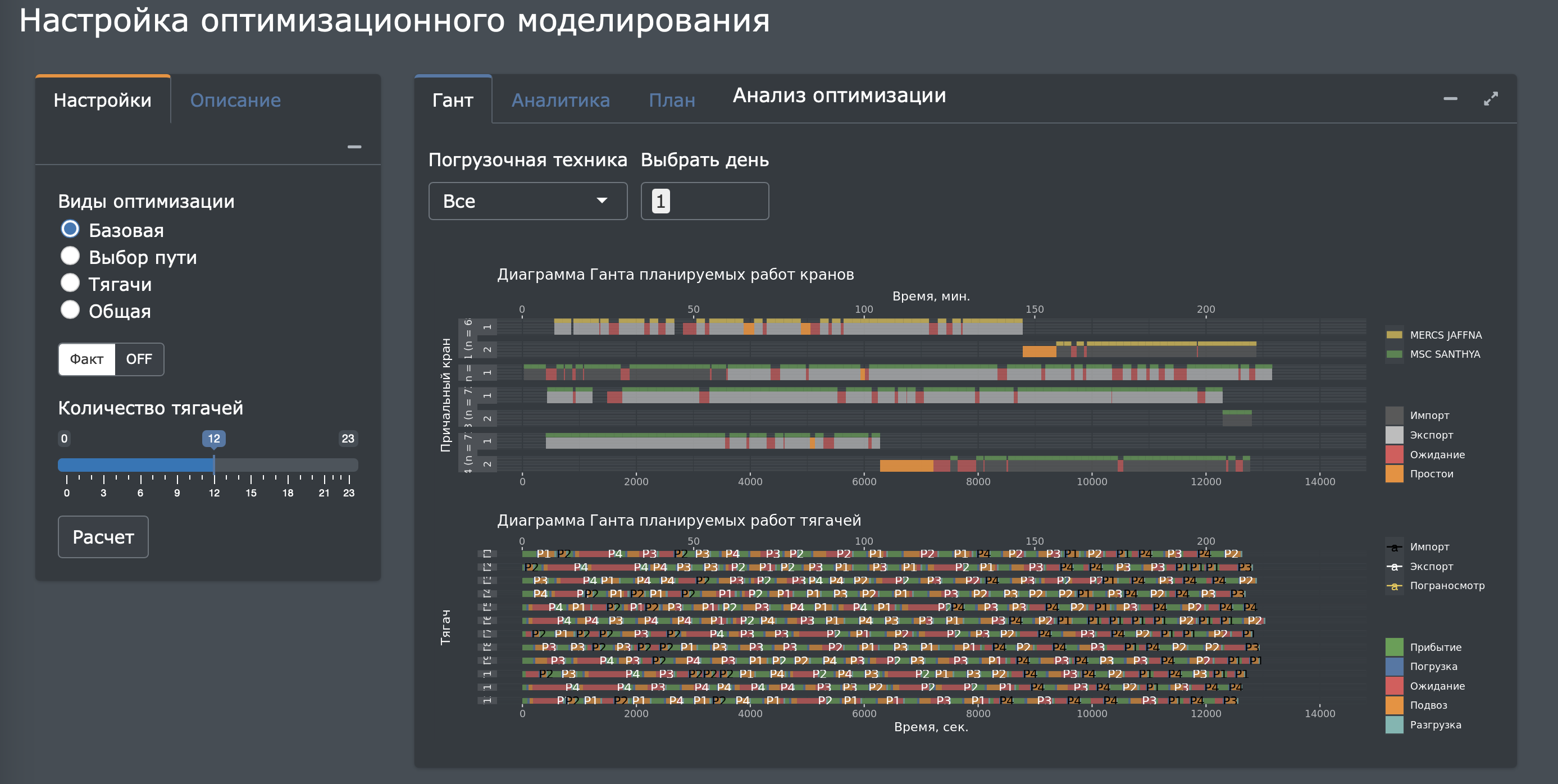
Разработка математической оптимизационной модели позволила сократить потребность в производственных фондах на 30%, а также уменьшить порожняковый пробег на 10% за счёт автоматического назначения тягачей на рабочие задания. Таким образом, отдел производственного планирования получил возможность балансировать эффективность выполнения работ с точки зрения затрат и пропускной способности производственных мощностей.
Особенности реализации проектов математической оптимизации
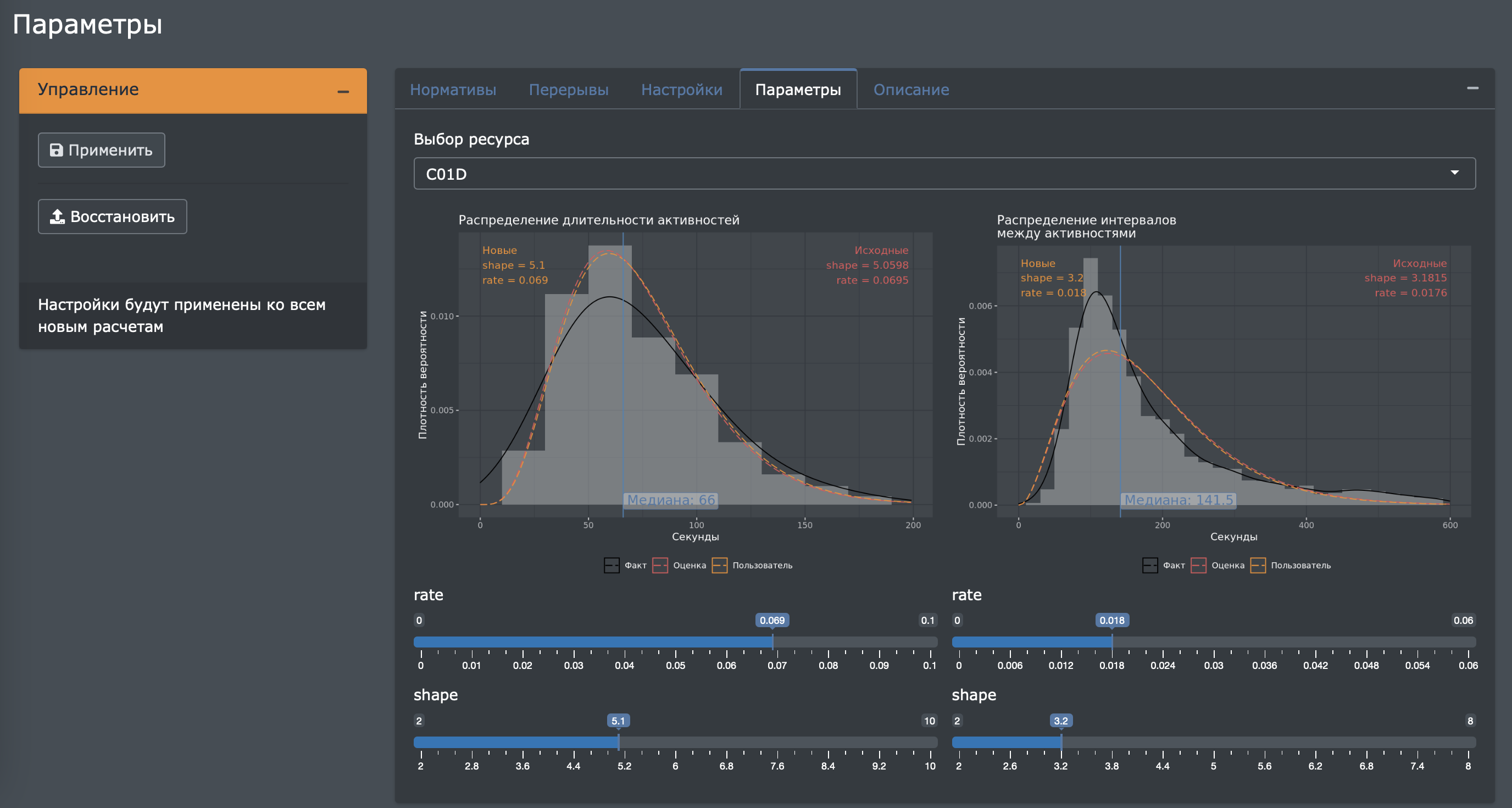
Наравне с классическими методами математической оптимизации (линейные и целочисленные задачи, нелинейные задачи, стохастические и вероятностные задачи, динамические задачи, комбинаторные задачи) могут быть использованы передовые методы оптимизации на базе обучения с подкреплением (Reinforcement Learning) и глубокого обучения нейронных сетей (Deep Learning), что открывает новые технологические перспективы в области оптимизации операционных решений.
Предполагаемые этапы проекта:
- Исследование предметной области и поиск потенциала роста эффективности, подготовка аналитического отчёта
- Подготовка минимального функционального прототипа для тестирования гипотез о возможности оптимизации, подготовка финансового обоснования реализации проекта
- Разработка архитектуры и дизайна комплексного решения
- Итеративная разработка решения с возможностью корректировки показателей эффективности работы и функционального контура оптимизации
- Развёртывание решения и интеграция с инфраструктурой заказчика
- Подготовка эксплуатационной документации и передача на поддержку